AVL Tree

AVL TREE

AVL Tree is an expert balancing of Binary Search Tree where the difference between heights of left and right can't be more than one or all nodes. 

Why should we use AVL Tree than Binary Search Tree?

Almost all of Binary Search Tree operations take O(n) time to process all its data. But, we know that AVL Tree operations take O(log n) time to process all its data. So as we know, AVL Tree can handle data more useful than Binary Search Tree.

Example of Binary Search Tree (NOT AVL Tree)

Example of AVL Tree

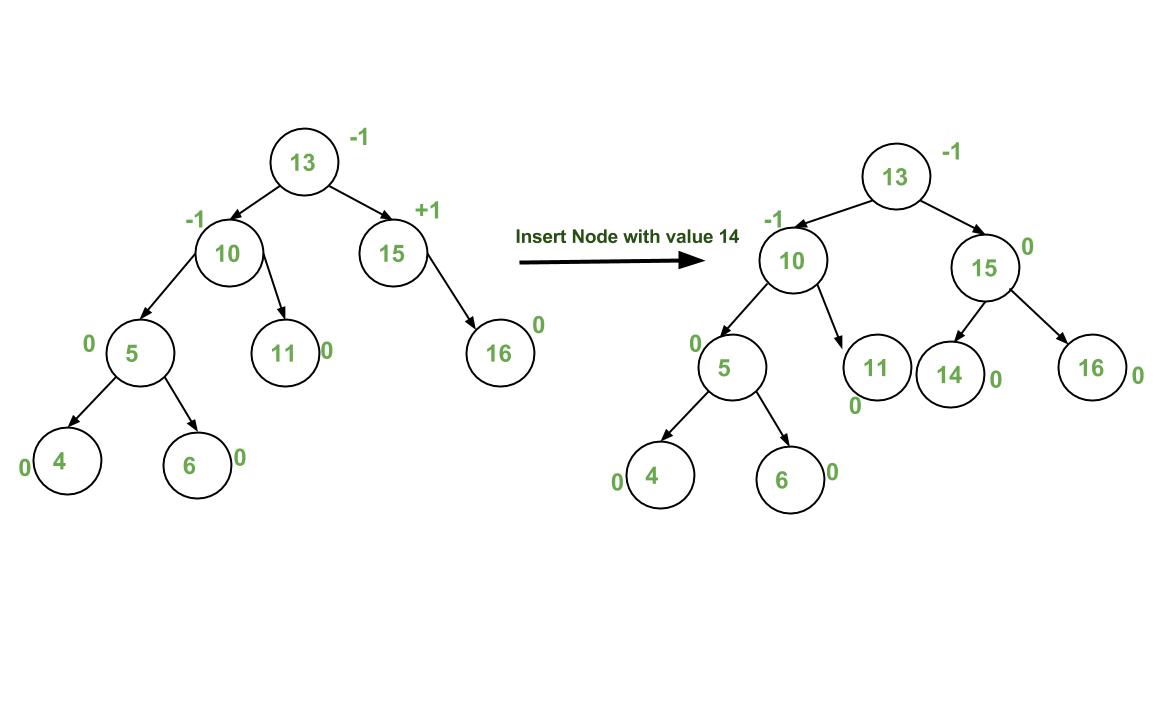
INSERTION

To make sure that the given tree remains AVL after every insertion, we must augment the standard Binary Search Tree insert operation to perform some re-balancing. Following are two basic operations that can be delivered to re-balance a Binary Search Tree without violating the Binary Search Tree property (keys(left) < key(root) < keys(right)).

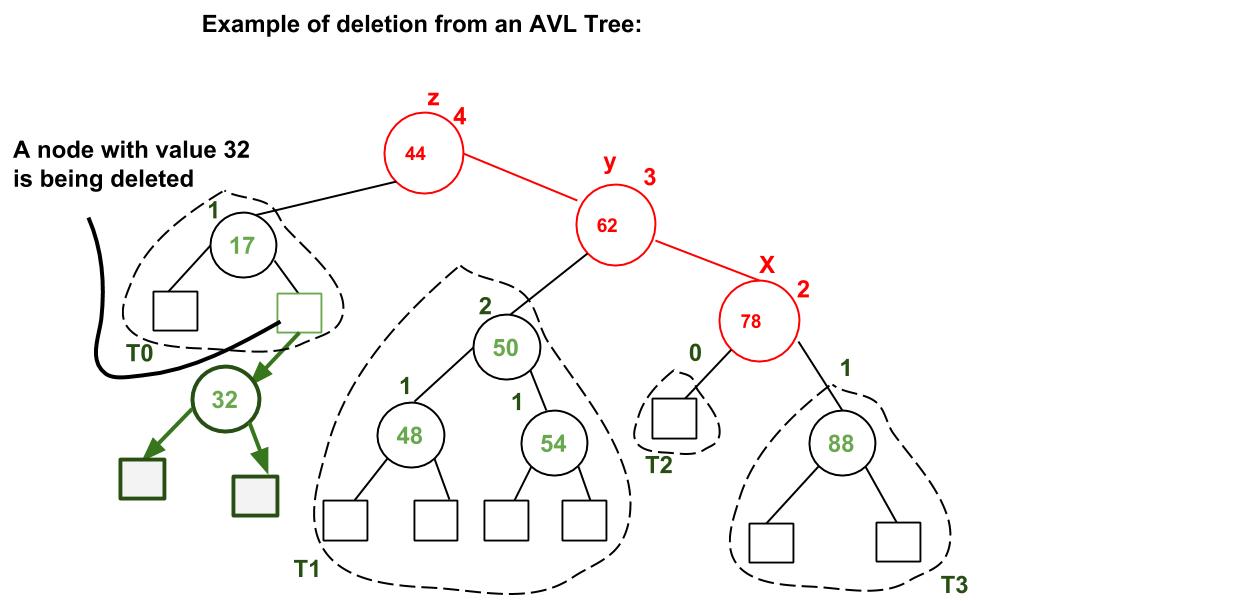
DELETION

To make sure that the given tree remains AVL after every deletion, we must augment the standard BST delete operation to perform some re-balancing. Following are two basic operations that can be performed to re-balance a BST without violating the BST property (keys(left) < key(root) < keys(right)).

REFERENCES: https://www.geeksforgeeks.org/avl-tree-set-1-insertion/?ref=lbp
                           https://www.geeksforgeeks.org/avl-tree-set-2-deletion/?ref=lbp